
1. 이론
KMP 알고리즘이란, 문자열 탐색 알고리즘으로써 알고리즘을 만든 사람들(Knuth-Morris-Pratt)의 앞글자를 딴 것이다.
웹페이지에서 ctrl + F를 이용하여 문자열을 검색할 때, 특정 단어를 검색엔진에서 검색할때도 사용될 수 있다.
해당 알고리즘의 시간복잡도는 O(N+M)을 가진다.
2. 구현
KMP 알고리즘은 접두사(prefix)와 접미사(suffix)의 개념을 활용하여 실패함수 테이블을 만들고, 테이블을 활용하여 반복되는 문자열을 건너뛰면서 패턴을 찾는 알고리즘이다.
접두사와 접미사에 대해 간단하게 정리해보고자 예를 들어보겠다.
"abacabab"라는 문자열이 있다고 가정하자.
우리는 각 문자의 길이에 따라 접두사와 접미사가 일치하는 최대 길이를 테이블에 저장할 것이다.
실패함수 테이블을 만드는 과정을 확인해보겠다.
접미사를 찾는 화살표는 뒤로 쭉 진행하게되고,
접두사를 찾는 화살표는 일치하지않으면 앞으로 되돌아오게된다.

1. 테이블의 처음은 0으로 채운다.

2. a와 b를 비교한다.
일치하지 않으므로 0으로 채운다

3. 인덱스 0번의 a와 인덱스 2번의 a가 일치한다.
일치하는 접두사 인덱스의 값에 +1을하여 테이블을 채워준다.

4. 인덱스 1번의 b와 3번의 c는 일치하지 않는다.
일치하지 않을 경우, 일치하지 않는 접두사(b)의 바로 이전 값(a)의 실패함수 테이블 값(0)의 인덱스로 돌아가서 현재 접미사의 문자와 일치하는지 확인한다.
위 과정을 일치하는 문자가 나올때까지 인덱스의 맨처음까지 반복한다.
되돌아간 인덱스 0의 문자 a와 c도 일치하지 않으므로, 실패함수 테이블에 0을 채워넣고 다음으로 넘어간다.
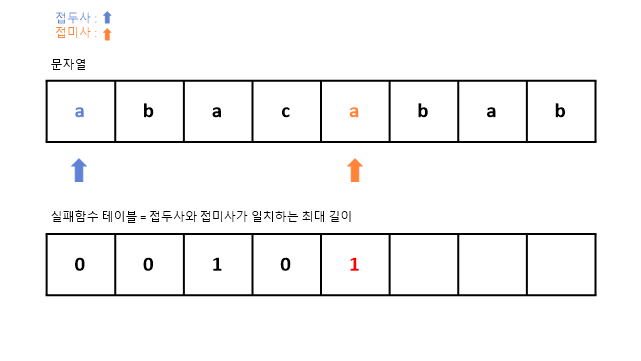
5. 인덱스 0번의 a와 인덱스 4번의 a가 일치한다.
일치하는 접두사 인덱스 값에서 +1을 하여 채워준다.
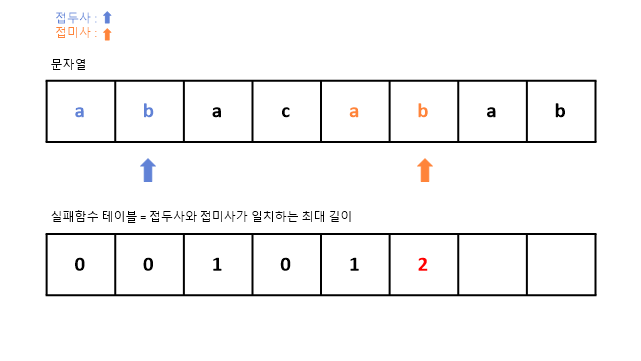
6. 인덱스 1번의 b와 인덱스 5번의 b가 서로 일치한다.
일치하는 접두사의 인덱스 값에서 1에서 +1을 하여 2를 테이블에 추가한다.
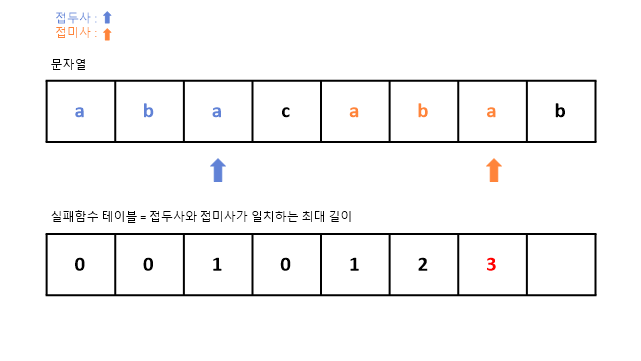
7. 인덱스 2번의 a와 인덱스 6번의 a가 서로 일치한다.
일치하는 접두사 인덱스 값인 2에서 +1을하여 3을 채워준다.
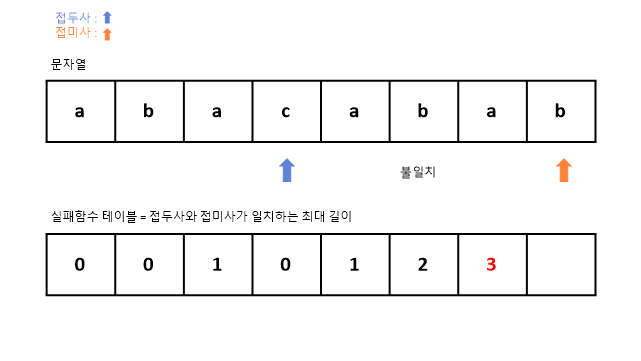
8. 인덱스 3번의 c와 인덱스 7번의 b가 서로 일치하지 않는다.
4번에서와 같이 실패함수 테이블에서 접두사의 이전 인덱스의 값을 참조하여 돌아간다.
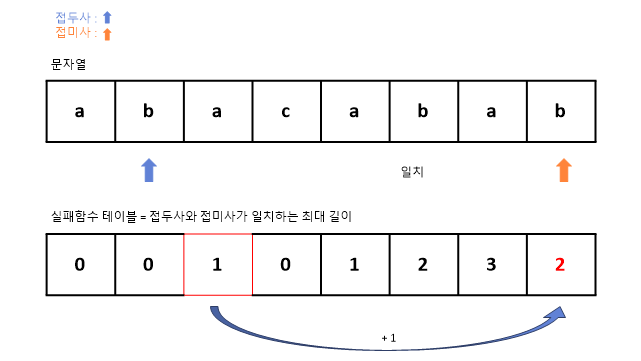
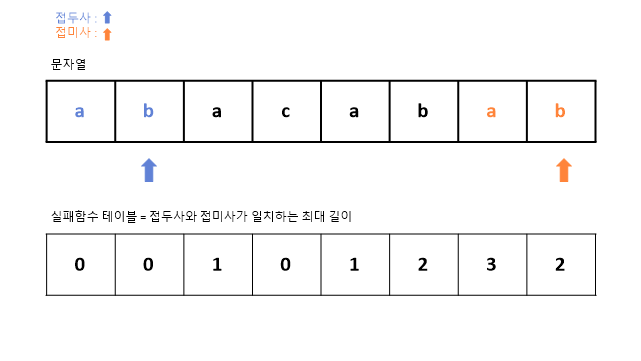
9. 돌아간 인덱스 1번의 문자 "b"와 7번 인덱스의 값 b가 서로 일치한다.
일치한다면 해당 실패함수 테이블의 값 1에 1을 더한 값인 2를 테이블에 추가한다.
실패함수 테이블을 이용하여 8-9번의 과정을 통해 우리는 맨앞에서부터 다시 문자열을 탐색하지 않고도 아래와 같이 일치하는 접두사와 접미사를 찾을수 있었다.
위에서 구한 실패함수 테이블을 이용하여 패턴을 찾는것이 KMP알고리즘이다.
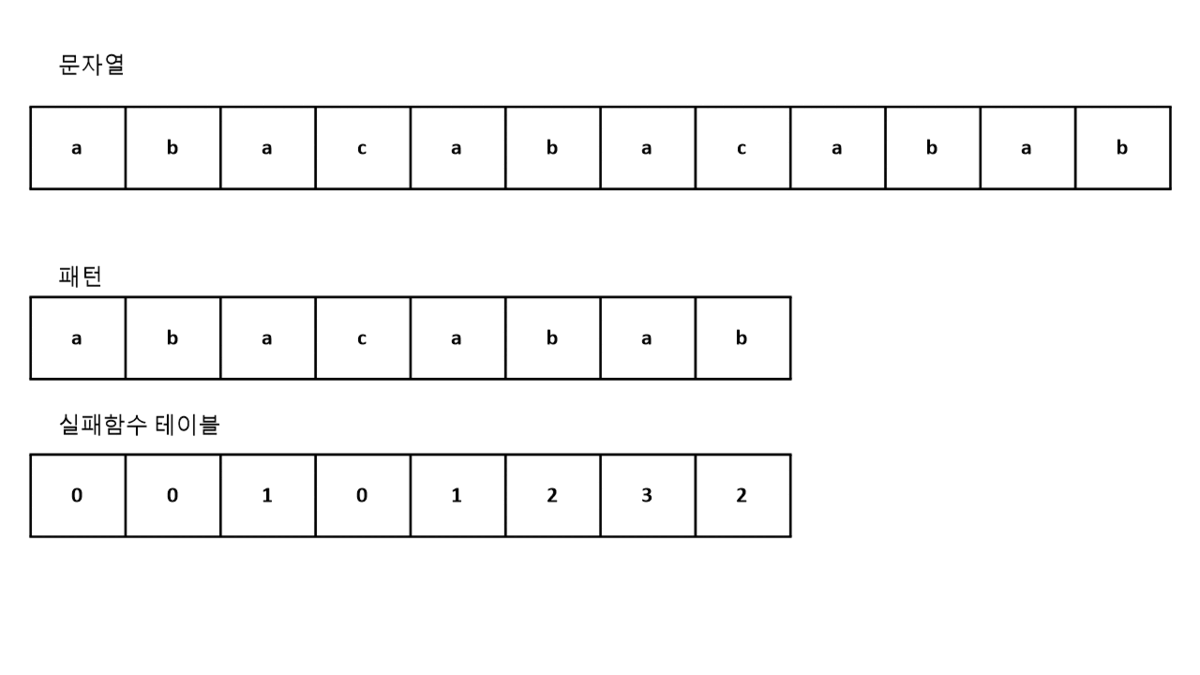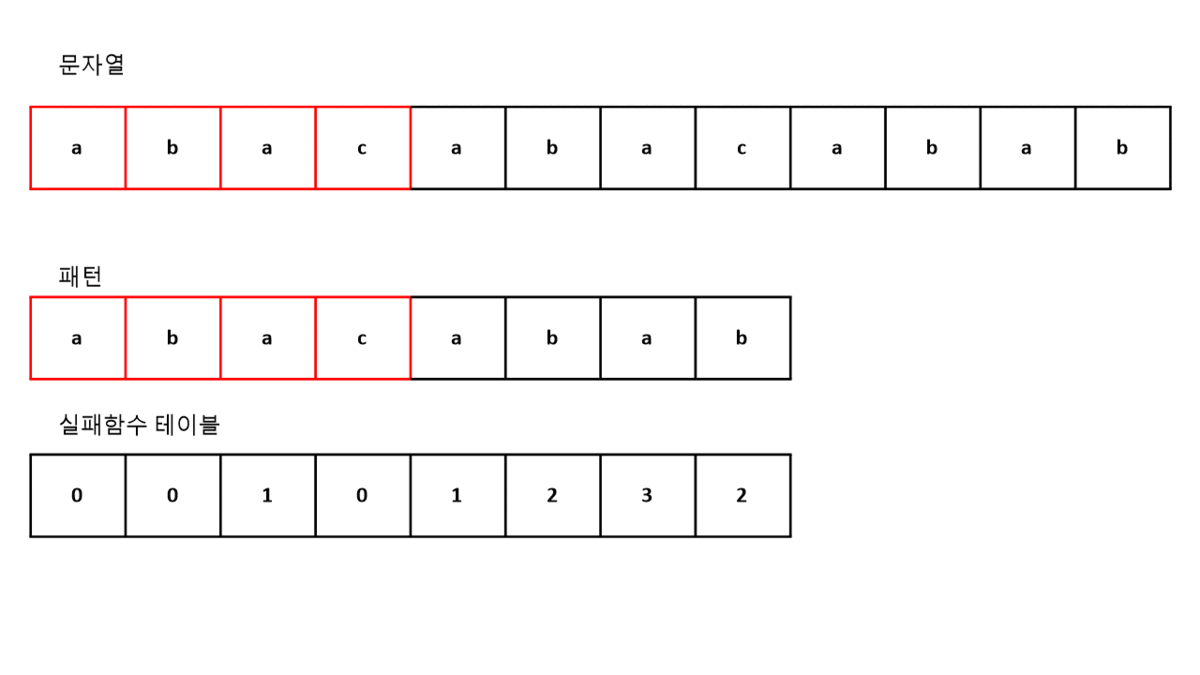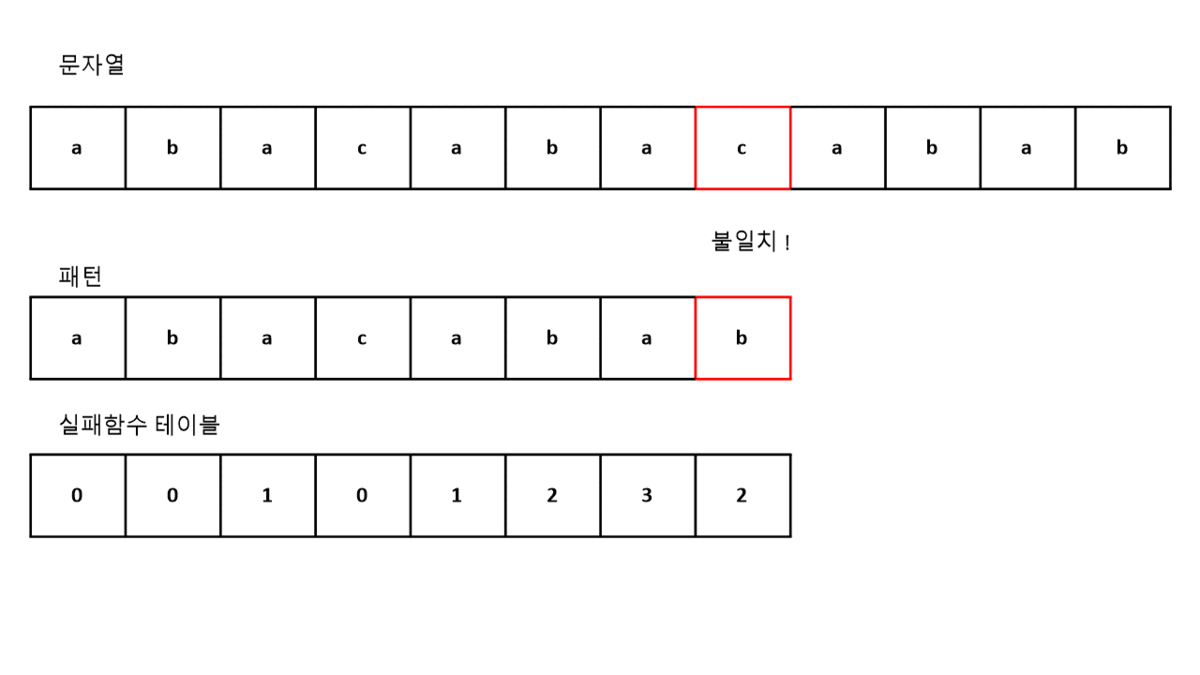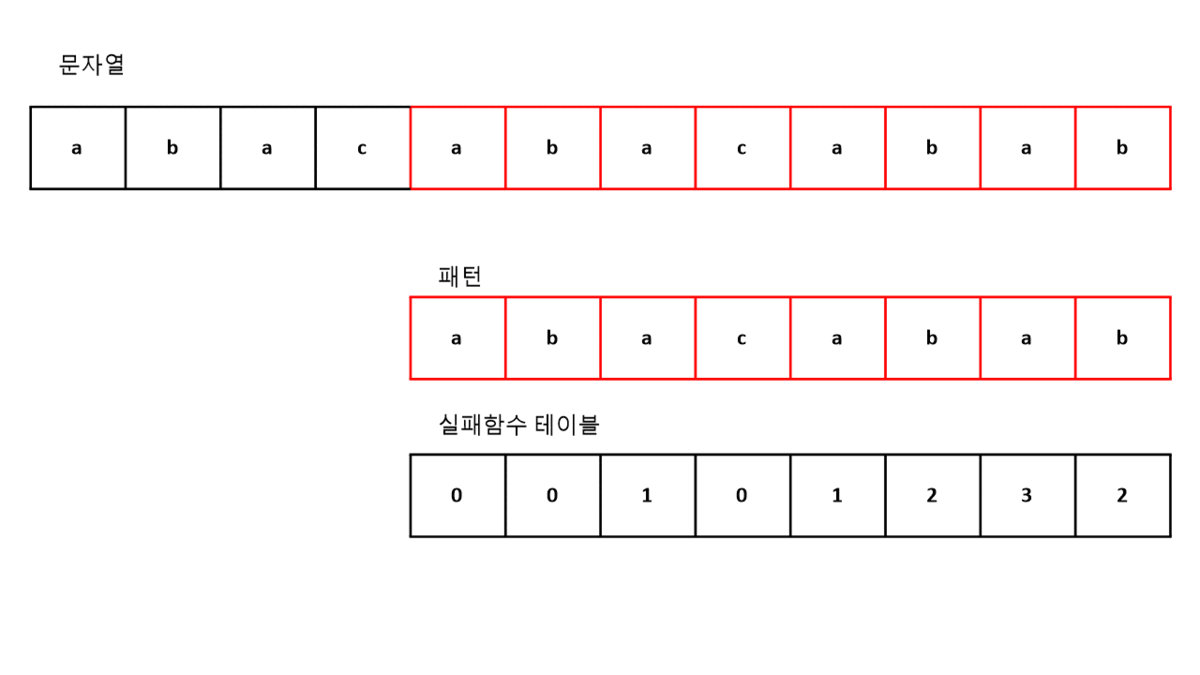
만약 우리에게 주어진 문자열이 "abacabacabab" 이고,
찾아야하는 패턴이 위 실패함수 테이블을 만든 문자열 "abacabab"라고 하자.
이때 우리는 실패함수 테이블을 아래와 같이 이용 할 수 있다.
3. 코드
#include <iostream>
#include <string>
#include <vector>
using namespace std;
vector<int> makeTable(string pattern)
{
int patternSize = pattern.length();
vector<int> table(patternSize, 0);
int j = 0;
for(int i = 1; i < patternSize; i++)
{
while(j > 0 && pattern[i] != pattern[j])
j = table[j-1];
if(pattern[i] == pattern[j])
{
table[i] = ++j;
}
}
return table;
}
void KMP(string s, string pattern)
{
vector<int> table = makeTable(pattern);
int sSize = s.length();
int patternSize = pattern.length();
int j = 0;
for(int i = 0; i < sSize; i++)
{
while(j > 0 && s[i] != pattern[j])
j = table[j-1];
if(s[i] == pattern[j])
{
j++;
if(j == patternSize)
{
cout << "Pattern Matched ! index : " << i - j + 2 << "\n";
j = table[j-1];
}
}
}
}
int main()
{
/*
ABC ABCDAB ABCDABCDABDE
ABCDABD
abacabacabababacabab
abacabab
ababacabacaabacaaba
abacaaba
*/
string s = "abacabacabababacabab";
string pattern = "abacabab";
KMP(s,pattern);
}
'Problem Solving > Algorithm' 카테고리의 다른 글
| [Algorithm] - 문자열 검색 알고리즘 : Naive String Search (0) | 2022.10.21 |
|---|---|
| [Algorithm] - Topology Sort(위상정렬) (0) | 2022.10.12 |
| [Algorithm] - Dijkstra(다익스트라) 알고리즘 (0) | 2022.10.02 |
| [Algorithm] - Kruskal's Algorithm(최소 스패닝 트리) (0) | 2022.09.13 |
| [Algorithm] - Union-Find(Disjoint-set) (0) | 2022.09.13 |