
이론
Dijkstra(다익스트라) 알고리즘이란, 그래프의 한 정점에서 모든 정점까지의 최단 거리를 각각 구하는 알고리즘(최단경로 문제)이다.
처음 작성된 알고리즘은 시간복잡도 O(N^2)을 가지는데, 이후 우선순위큐(=힙트리)를 이용한 개선 알고리즘이 나오면서 O(NlogN)으로 개선되었다.
다익스트라의 특징은 음의 가중치가 없다는 점이다. 따라서 현실세계에 적용할 수 있는 효율적인 알고리즘이라고 할 수 있다.
그래프의 방향은 상관없으나, 가중치가 하나라도 음수라면 다익스트라 알고리즘을 사용할 수 없다.
이때는 조건에따라 벨만-포드 알고리즘을 사용하여 최단거리를 구할 수 있다.
또한, 다익스트라 알고리즘은 하나의 노드로부터 최단 경로를 구하는 알고리즘인 반면, 플로이드-워셜 알고리즘은 가능한 모든 노드쌍들에 대한 최단거리를 구하는 알고리즘이다.
게임 개발 등에서 자주 사용하는 A* 알고리즘은 다익스트라의 확장판이라고 할 수 있다.
구현
두가지 방법 모두 구현해보도록 하자.
* O(N^2)
1. 출발점으로부터의 최단거리를 저장할 배열 d[n]을 만들고, d[1]에는 0, 나머지에는 최대값(ex.INT_MAX)을 넣어준다.
2. 노드의 방문 여부를 판단할 배열 v[n]을 만들고 0으로 초기화해준다.
3. 현재 노드(A)에서 갈 수 있는 노드중 비용이 가장 적은 노드(B)를 방문하고,
d[B] > d[A] + P[A][B] 일 경우, 즉 A->B로 가는 경우의 비용이 더 작다면 갱신하고 A에 방문 처리를 한다.
4. 방문하지 않은 노드들 중, 비용이 제일 적은 노드를 하나 골라 3번의 과정을 반복한다.
5. 모든 노드가 방문 상태가될때까지 반복한다.
위의 과정을 마치면 배열 d[i]에 저장되는 값이 바로 출발점에서부터 i노드까지의 최단거리이다.
나무위키에 괜찮은 예제가 있어서 가져왔다.
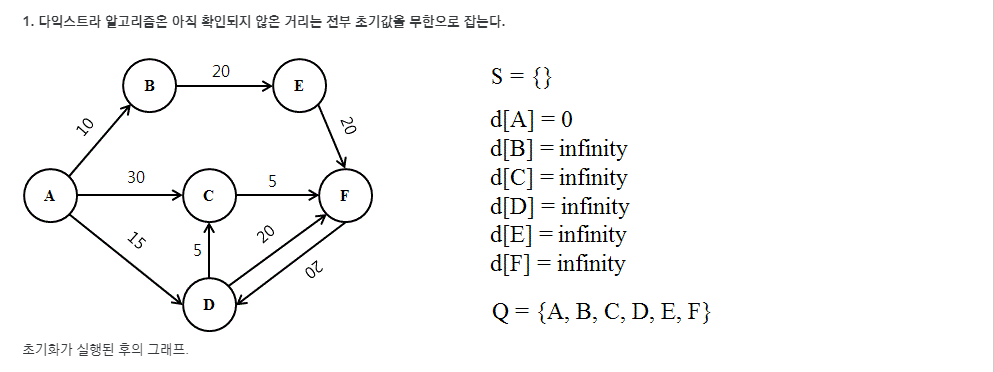

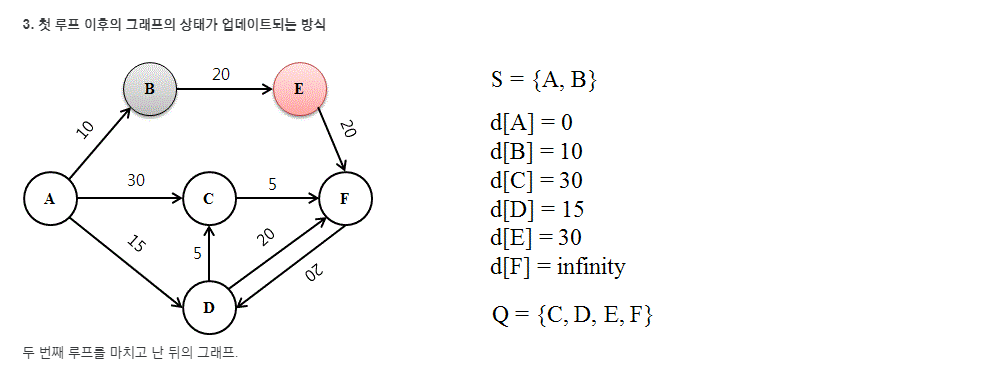
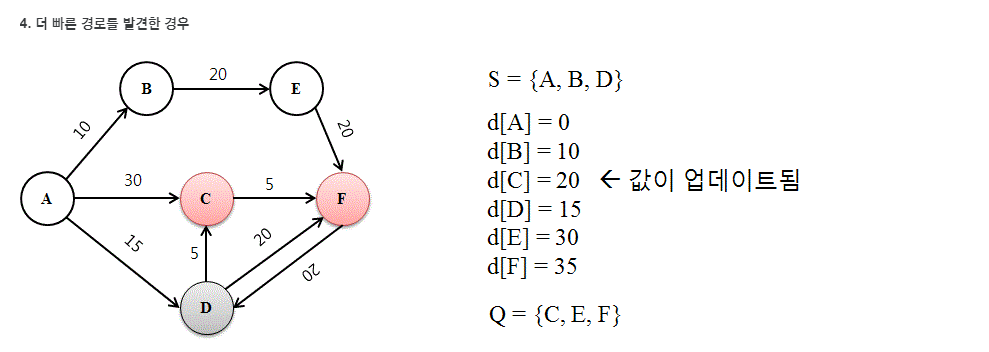
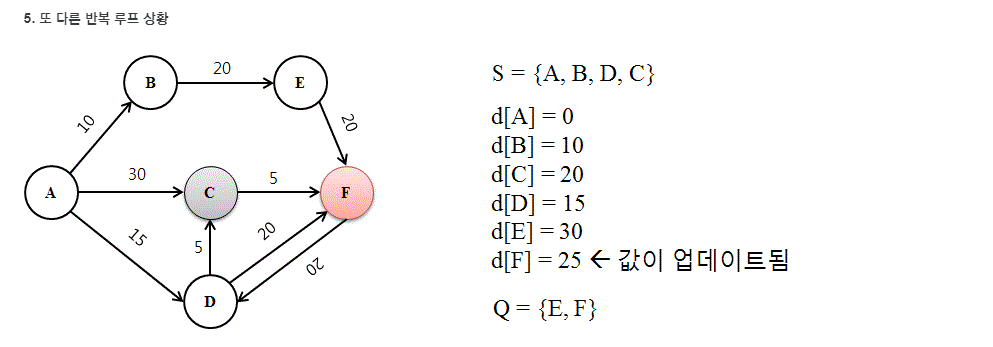

위의 예제를 코드로 작성한다면 아래와 같다.
#include <iostream>
#include <vector>
using namespace std;
#define INF 10000
#define NUMBER 6
vector<vector<int>> a = {
{0, 10, 30, 15, INF,INF},
{INF,0,INF,INF,20,INF},
{INF,INF,0,INF,INF,5},
{INF,INF,5,0,INF,20},
{INF,INF,INF,INF,0,20},
{INF,INF,INF,20,INF,0}
};
vector<int> d(NUMBER,INF);
vector<int> v(NUMBER,0);
void dijkstra(int startNode)
{
for(int i =0; i < NUMBER; i++)
{
d[i] = a[startNode][i];
}
v[startNode] = true;
for(int i =0; i< NUMBER-2; i++) // NUMBER -2 를 하는 이유는 자기자신과 마지막 노드는 방문하지 않아도 되기 때문이다.
{
int min = INF;
int index = 0;
for(int j = 0; j < NUMBER; j++)
{
if(!v[j] && d[j] < min)
{
min = d[j];
index = j;
}
}
v[index] = true;
for(int j = 0; j < NUMBER; j++)
{
if(!v[j])
{
if(d[j] > d[index] + a[index][j] )
{
d[j] = d[index] + a[index][j];
}
}
}
}
}
int main()
{
dijkstra(0);
for(int i =0; i < NUMBER ; i++)
{
printf("%d\n", d[i]);
}
}실행해보면 나오는 결과와 위 예제의 값이 동일한것을 확인 할 수있다.
* O(NlogN)
우선순위 큐를 이용하여 시간복잡도를 개선할 수 있다.
1. 위 로직과 같이 최소비용을 저장할 배열 d[N]을 만들고, d[1]에는 0, 나머지에는 큰 값을 넣어준다.
방문을 위한 배열은 만들 필요 없다.
2. 각 노드의 간선 정보를 저장할 vector<pair<int,int>>를 노드 개수대로 만들고, 노드 인덱스에 간선 정보(연결된 노드, 비용)를 추가한다.
3. 우선순위 큐를 생성한다. priority_queue<pair<int,int>> 를 만든다. pair의 첫번째는 비용, 두번째는 노드 인덱스를 집어 넣을 용도다.
4. 큐에 {0,시작노드}를 넣고 큐가 빌때까지 아래 로직을 반복한다.
5. 큐의 맨 앞의 값을 빼내어 변수에 저장한다. 위에서 설명한대로 두번째 값은 연결된 노드이고, 첫번째 값은 해당 노드로 넘어갈때 드는 비용이다.
6. priority_queue의 최대힙을 사용하여 비용이 적은것부터 보기 위해서 비용을 음수화해준다.
최대힙은 기준이 되는 pair의 첫번째가 더 큰 값을 시작으로 내림차순이 된다.
만약 같다면 두번째가 큰 순서로 내림차순 된다.
위의 내용을 토대로 음수화를 해준다면 -1 > -5 이므로 비용이 적은것대로 정렬할 수 있다.
그렇게 하기 위해서 5번에서 첫번째에 비용을 넣어줬다.
큐에서 꺼낼때도 -를 꼭 붙여주어야 한다.
7. 현재 확인한 비용이 저장된 최단거리보다 크다면 넘어간다.
8. 저장된 최단거리보다 작다면 반복문을 통해 인접노드로 거쳐서 가는 비용을 확인해서 기존 최소 비용보다 작다면 갱신해주고, {-비용,인접노드} 순서로 큐에 넣어준다.
위의 과정을 지나면, 배열 d[i]에는 i노드에 도착하는 최소비용이 저장되어 있을 것이다.
코드는 아래와 같다.
O(N^2)에서 했던 예제와 동일한 상황으로 테스트했다.
#include <iostream>
#include <vector>
#include <queue>
#define INF 100000
#define NUMBER 6
using namespace std;
vector<int> d(NUMBER+1, INF);
vector<pair<int,int>> a[NUMBER+1];
int dijkstra(int startNode) {
d[1] = 0 ;
priority_queue<pair<int,int>> pq; // (time, city)
pq.push(make_pair(0,1));
while(pq.empty() == false)
{
int distance = -pq.top().first;
int city = pq.top().second;
pq.pop();
if(d[city] < distance) continue;
for(int i =0; i < a[city].size(); i++)
{
int nextCity = a[city][i].first;
int nextDistance = distance + a[city][i].second;
if(nextDistance < d[nextCity])
{
d[nextCity] = nextDistance;
pq.push(make_pair(-nextDistance, nextCity));
}
}
}
}
int main()
{
d[1] = 0;
a[1].push_back(make_pair(2,10));
a[1].push_back(make_pair(3,30));
a[1].push_back(make_pair(4,15));
a[2].push_back(make_pair(5,20));
a[3].push_back(make_pair(6,5));
a[4].push_back(make_pair(3,5));
a[4].push_back(make_pair(6,20));
a[5].push_back(make_pair(6,20));
a[6].push_back(make_pair(4,20));
dijkstra(1);
const char* alpha = "0ABCDEF";
for(int i =1; i <= NUMBER; i++)
{
printf("%c : %d\n", alpha[i], d[i]);
}
}실행한 결과는 O(N^2)와 동일하게 출력되었다.
* 경로 추적
다익스트라 알고리즘을 이용하여 각 노드로 접근했을때의 비용은 위 내용을 통해 알아보았다.
하지만, 위처럼 최소비용, 최단거리일때 어떠한 경로를 가지는지 알고 싶을때가 있을것이다.
경로을 추적하는 것만 추가하고 이번 포스트는 마무리 하도록 하겠다.
추가하는 내용은 간단하다.
경로를 저장해줄 trace라는 배열을 선언해준다.
위의 다익스스트라 알고리즘에서 노드를 갱신해줄때 trace[다음노드] = 현재 노드 와 같이 값을 넣어준다.
값을 저렇게 넣어 주었을때, 우리가 찾고자하는 목적지 노드의 인덱스 k를 trace[k]와 같이 넣었을때,
k로 접근하는 이전 노드의 인덱스를 반환해준다.
이런식으로 경로를 역으로 추적할 수 있다.
코드는 아래와 같다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <stack>
#define INF 100000
#define NUMBER 6
using namespace std;
vector<int> d(NUMBER+1, INF);
vector<pair<int,int>> a[NUMBER+1];
vector<int> trace(NUMBER+1, 0);
int dijkstra(int startNode) {
d[1] = 0 ;
priority_queue<pair<int,int>> pq; // (time, city)
pq.push(make_pair(0,1));
while(pq.empty() == false)
{
int distance = -pq.top().first;
int city = pq.top().second;
pq.pop();
if(d[city] < distance) continue;
for(int i =0; i < a[city].size(); i++)
{
int nextCity = a[city][i].first;
int nextDistance = distance + a[city][i].second;
if(nextDistance < d[nextCity])
{
d[nextCity] = nextDistance;
pq.push(make_pair(-nextDistance, nextCity));
trace[nextCity] = city; //경로를 파악하기 위한 추가 코드
// trace라는 배열을 역추적하여 전체 경로를 파악하기 위함이다.
}
}
}
}
int main()
{
d[1] = 0;
a[1].push_back(make_pair(2,10));
a[1].push_back(make_pair(3,30));
a[1].push_back(make_pair(4,15));
a[2].push_back(make_pair(5,20));
a[3].push_back(make_pair(6,5));
a[4].push_back(make_pair(3,5));
a[4].push_back(make_pair(6,20));
a[5].push_back(make_pair(6,20));
a[6].push_back(make_pair(4,20));
dijkstra(1);
const char* alpha = "0ABCDEF";
//실제 역추적하는 코드
vector<stack<int>> vPath(NUMBER+1);
for(int i =1; i <= NUMBER; i++)
{
printf("%c : %d\n", alpha[i], d[i]);
int bt = trace[i];
// trace[i]가 가지고 있는 값은 i의 노드로 접근한 이전 노드의 인덱스가 들어있다.
// 따라서 이전 경로를 계속 역으로 추적하고 있다.
// 이를 backtracking이라고 한다.
while(bt != 0)
{
vPath[i].push(bt);
bt = trace[bt]; // stack에 역으로 된 경로를 쌓아준다.
}
printf("\n");
}
//위에서 경로를 쌓은 stack을 출력한다.
for(int i = 1; i <= NUMBER; i++)
{
while(vPath[i].empty() == false)
{
int tempTop = vPath[i].top();
vPath[i].pop();
if(vPath[i].empty() == false)
{
printf("%c%s", alpha[tempTop], "->");
}
else
{
printf("%c->%c\n", alpha[tempTop], alpha[i]);
break;
}
}
}
}출처 :
'Problem Solving > Algorithm' 카테고리의 다른 글
| [Algorithm] - 문자열 검색 알고리즘 : Naive String Search (0) | 2022.10.21 |
|---|---|
| [Algorithm] - Topology Sort(위상정렬) (0) | 2022.10.12 |
| [Algorithm] - Kruskal's Algorithm(최소 스패닝 트리) (0) | 2022.09.13 |
| [Algorithm] - Union-Find(Disjoint-set) (0) | 2022.09.13 |
| [Algorithm] - LIS(Longest Increasing Subsequence) (0) | 2022.08.19 |