
이론
크러스컬 알고리즘은 Union-Find 알고리즘을 사용하기때문에 만약 Union-Find에 대해 잘 모른다면
[Algorithm] - Union-Find(Disjoint-set)
이론 여러개의 집합이 존재 할때, 두개의 집합을 선택해서 같은 그래프에 속하는지 판단하는 알고리즘이다. 간단하게 이야기 하자면, 교집합이 있다면 한개의 집합으로 보게 하겠다는 의미이다
mocha-bro.tistory.com
위 포스트를 한번 읽고 오면 이해하는데 수월 할 수 있다.
크러스컬 알고리즘? 크루스칼 알고리즘?을 정리해보려고 한다.
위 알고리즘의 이론은 최소 비용으로 신장 부분 트리(Spanning SubTree)를 찾는 알고리즘이다.
아래 나무위키에 크러스컬 알고리즘의 단계 별 예제가 있어서 가져왔다.
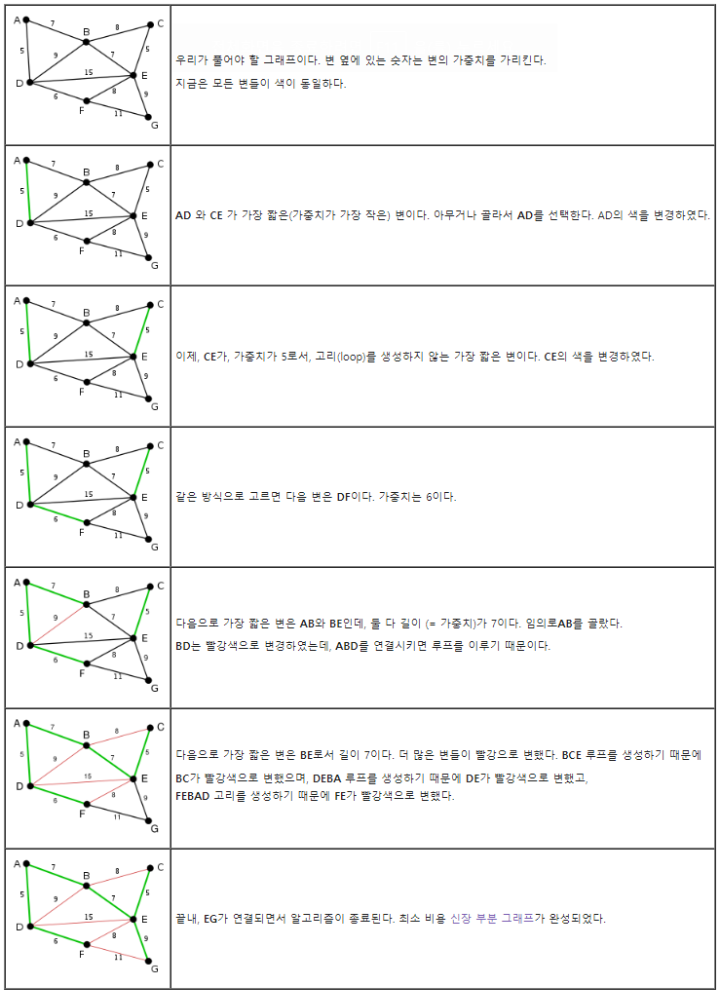
간단하고 설명이 잘되어있는것 같아 가져왔다.
위 설명의 핵심은 아래와 같다.
1. 비용을 기준으로 정렬한다.
2. 선택하지 않은 간선 중 사이클을 발생시키지 않으면서 최소 비용을 선택하여 그래프를 연결한다.
3. 모든 간선을 탐색한다.
위의 과정을 진행하면, 최소 비용을 가지는 모든 노드를 포함하는 그래프를 완성 할 수 있다.
2번에서 사이클 발생 여부는 이 전 포스트에서 작성한 Union-Find 알고리즘을 사용하게 된다.
구현
우선, 간선을 표현할 구조체를 Edge라는 이름으로 정의한다.
구조체에는 연결하는 노드들(v1,v2),비용(cost)가 포함된다.
1. 구조체를 비용을 기준으로 오름차순으로 정렬 한다.
2. Union-Find 알고리즘을 그대로 사용하여 각각의 노드들이 같은 집합 안에 포함되는지 확인한다.
3. 포함된다면 이미 해당 노드는 연결되어 있는것이고, 사이클이 발생 할 수 있으므로 다음 비용을 가지는 간선으로 넘어간다.
4. 포함되지 않는다면 집합에 포함시키고, 현재 간선의 비용을 누적시킨다.
5. 모든 간선을 확인했다면 완료
코드
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
vector<int> unf(4951);
struct Edge{
int v1_;
int v2_;
int cost_;
Edge(int v1, int v2, int cost) : v1_(v1), v2_(v2), cost_(cost) {}
bool operator<(Edge& b)
{
return cost_ < b.cost_;
}
};
int parentFind(int a)
{
if(a == unf[a]) return a;
else return unf[a] = parentFind(unf[a]);
}
void parentUnion(int a, int b)
{
a = parentFind(a);
b = parentFind(b);
if(a != b) unf[a] = b;
}
int solution(int n, vector<vector<int>> costs) {
int answer = 0;
vector<Edge> v;
int costSize = costs.size();
for(int i =0; i < costSize; i++)
{
v.push_back(Edge(costs[i][0],costs[i][1],costs[i][2]));
}
for(int i =0; i <= n; i++)
{
unf[i] = i;
}
sort(v.begin(), v.end());
for(int i =0; i < costSize; i++)
{
int parentV1 = parentFind(v[i].v1_);
int parentV2 = parentFind(v[i].v2_);
if(parentV1 != parentV2)
{
parentUnion(v[i].v1_, v[i].v2_);
answer += v[i].cost_;
}
}
return answer;
}'Problem Solving > Algorithm' 카테고리의 다른 글
| [Algorithm] - 문자열 검색 알고리즘 : Naive String Search (0) | 2022.10.21 |
|---|---|
| [Algorithm] - Topology Sort(위상정렬) (0) | 2022.10.12 |
| [Algorithm] - Dijkstra(다익스트라) 알고리즘 (0) | 2022.10.02 |
| [Algorithm] - Union-Find(Disjoint-set) (0) | 2022.09.13 |
| [Algorithm] - LIS(Longest Increasing Subsequence) (0) | 2022.08.19 |