
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
[문제 설명]
좌표평면을 좋아하는 진수는 x축과 y축이 직교하는 2차원 좌표평면에 점을 찍으면서 놀고 있습니다. 진수는 두 양의 정수 k, d가 주어질 때 다음과 같이 점을 찍으려 합니다.
- 원점(0, 0)으로부터 x축 방향으로 a*k(a = 0, 1, 2, 3 ...), y축 방향으로 b*k(b = 0, 1, 2, 3 ...)만큼 떨어진 위치에 점을 찍습니다.
- 원점과 거리가 d를 넘는 위치에는 점을 찍지 않습니다.
예를 들어, k가 2, d가 4인 경우에는 (0, 0), (0, 2), (0, 4), (2, 0), (2, 2), (4, 0) 위치에 점을 찍어 총 6개의 점을 찍습니다.
정수 k와 원점과의 거리를 나타내는 정수 d가 주어졌을 때, 점이 총 몇 개 찍히는지 return 하는 solution 함수를 완성하세요.
제한사항
- 1 ≤ k ≤ 1,000,000
- 1 ≤ d ≤ 1,000,000
입출력 예
| k | d | result |
| 2 | 4 | 6 |
| 1 | 5 | 26 |
[문제 풀이]
문제 풀이 내용은 좀 수학적으로 접근해야했다.
처음에 2중 반복문을 통해 문제를 풀었는데 시간초과가 나면서 틀렸다.
방법을 찾다보니 좋은 방법이 있었다.
x 또는 y 둘 중 하나를 k씩 증가시키면서 다른 좌표축의 최댓값을 구하는 것이였다.
1번 예제를 통해 예를 들어보겠다.
1. x를 0부터 d까지 k씩 증가시킨다.
2. 각 x의 값에 대한 y값의 최댓값을 구한다.
=> 계산은 피타고라스를 이용한다. d^2 = x^2 + y^2, 우리가 알고싶은 값은 y 값이므로 y^2 = d^2 - x^2으로 변환하여 계산한다.
3. 2번에서 계산된 y^2에 제곱근을 구한 값이 해당 x에 대한 y의 최댓값이다. 이 y값을 k로 나누어주면 해당 x값으로 찍을 수 있는 y 값 좌표의 갯수가 나온다. 이때 나눗셈으로 계산하기때문에 y가 0일때가 제외되므로 계산된 값에 +1을 해준다.
4. x가 d보다 커질때까지 1~3번 과정을 반복한다.
처음에 글로만 봤을땐 이해가 잘 안됐다.
아래 그림으로 정리한 내용을 첨부했다. 이해하는데 도움이 되었다.
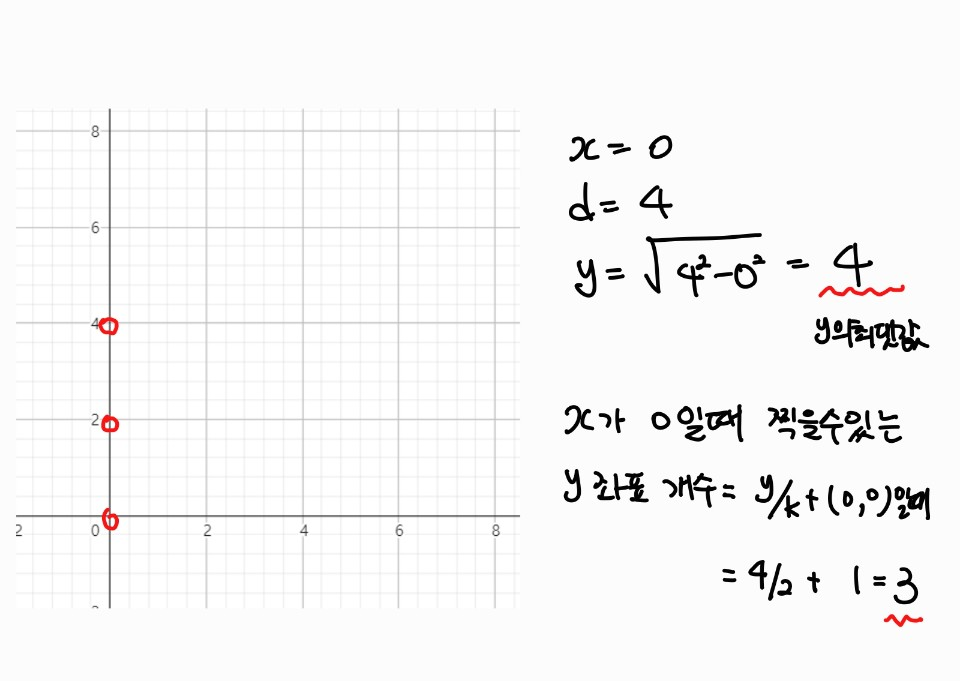
따라서 예제 1번 k = 2, d = 4일때 찍을수 있는 점의 개수는
x가 0일때 3개 (빨간 점)
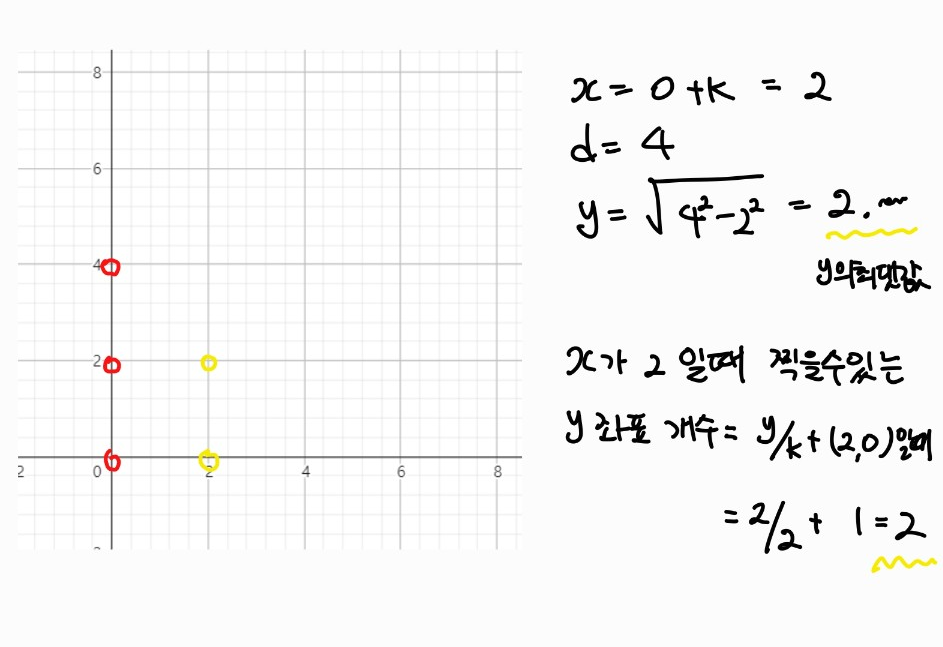
x가 2일때 2개 (노란 점)
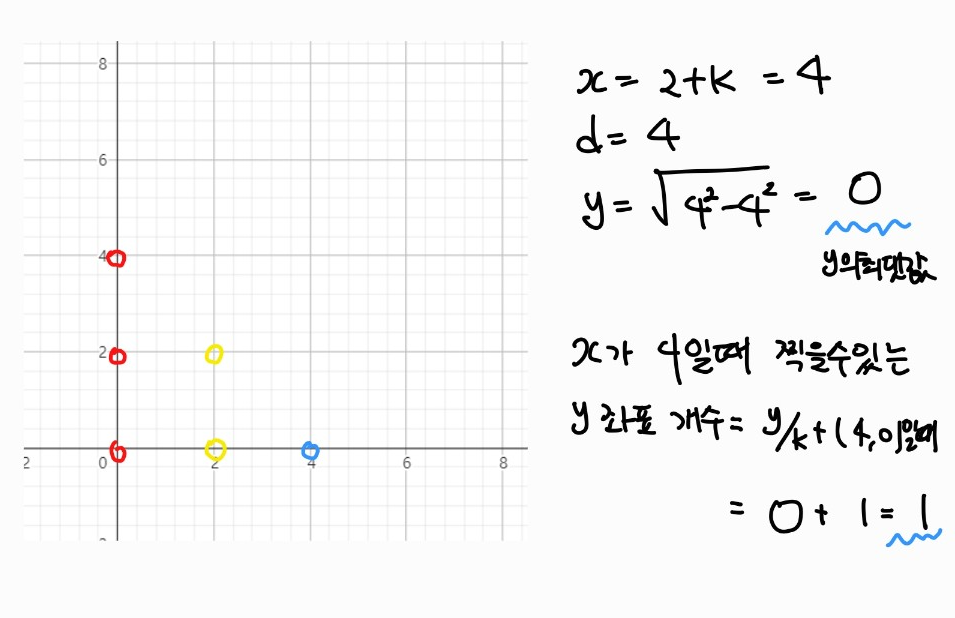
x가 4일때 1개 (파란 점)
총 6개이다.
다른 예제도 그림처럼 생각하면 된다.
c++의 경우 한가지 더 조심해야 할점은 리턴 사이즈가 long long이라는 것이다.
가급적 변수를 long long으로 선언해주는것이 좋다
입력으로 받는 d의 자료형이 int형이기때문에 제곱을 구할때 d*d의 범위가 int의 범위를 넘어간다.
이때 둘 중 하나의 d 앞에 (long long)으로 타입 변환을 해주면 정상적으로 연산 결과가 나온다.
int형 (산술연산) long long형 변수의 경우 연산의 결과값의 범위가 long long으로 나오기 때문이다.
이와는 별개로 int형과 double형의 연산 결과는 double형으로 나온다.
이 점 참고해서 풀면 정답처리가 될 것이다.
[코드]
[GitHub]
GitHub - EGyeom/ProblemSolving
Contribute to EGyeom/ProblemSolving development by creating an account on GitHub.
github.com
코드가 깨끗하고 명확하게 보일진 모르겠지만, 누군가에게 도움이 될 수도.. 있기에..
#include <string>
#include <vector>
#include <math.h>
using namespace std;
long long solution(int k, int d) {
long long answer = 0;
for(long long i = 0; i <= d; i += k)
{
long long sqr_d = (long long)d*d;
long long max_y = sqrt(sqr_d-(i*i))/k;
answer += (max_y + 1);
}
return answer;
}'Problem Solving > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] - 가장 큰 정사각형 찾기(C/C++) (0) | 2022.12.19 |
|---|---|
| [프로그래머스] - 구명보트(C/C++) (0) | 2022.12.16 |
| [프로그래머스] - 전력망 둘로 나누기(C/C++) (0) | 2022.12.14 |
| [프로그래머스] - 더 맵게(C/C++) (0) | 2022.12.13 |
| [프로그래머스] -[1차] 캐시(C/C++) (0) | 2022.12.12 |